HappyCpp

一个不会打代码的程序猿

0%

棋盘覆盖问题

发表于 更新于 分类于 阅读次数： 评论数：

棋盘覆盖问题

棋盘覆盖问题

这是算法课上老师讲的一道分治题目,题目描述如下：
在一个2^k*2^k个方格组成的棋盘中,若恰有一个方格与其他方格不同,则称该方格为一个特殊方格。

下图的棋盘是k=2时4*4的棋盘方格

用四种不同的L型骨牌去覆盖除特殊方格外的所有方格,且任何2个L型骨牌不得重叠覆盖。
这里,我们容易得到用到的L型骨牌数量为（4^k-1)/3;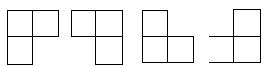

我们采用分治策略,将2^k*2^k的方格分成4个2^(k-1)*2^(k-1),如下图：

特殊方格必位于4个较小棋盘中,其余3个子棋盘中无特殊方格。
为了将这3个子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘
的汇合处,这3个子棋盘被L型骨牌覆盖的方格就成为该棋盘上的特殊方格。递归地使用这种分割,直至棋盘简化成1*1。如下图所示：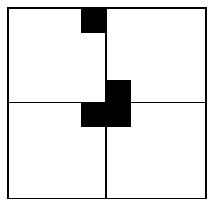

对于棋盘结构设计如下：
1、棋盘：可以用一个二维数组board[size][size]表示一个棋盘，其中，size=2^k。为了在递归处理的过程中使用同一个棋盘，将数组board设为全局变量；
2、子棋盘：整个棋盘用二维数组board[size][size]表示，其中的子棋盘由棋盘左上角的下标tr、tc和棋盘大小s表示；
3、特殊方格：用board[dr][dc]表示特殊方格，dr和dc是该特殊方格在二维数组board中的下标;
4、L型骨牌：一个2^k×2^k的棋盘中有一个特殊方格，所以，用到L型骨牌的个数为(4^k-1)/3，将所有L型骨牌从1开始连续编号，用一个全局变量tile表示。

我们先分析一层递归的情况：
我们创建一个函数void ChessBoard(int tr,int tc,int dr,int dc,int size);

我们创建一个变量s=size/2，用来分割棋盘
左上子棋盘左上角坐标为(tr,tc)
右上子棋盘左上角坐标为(tr,tc+s)
左下子棋盘左上角坐标为(tr+s,tc)
右下子棋盘左上角坐标为(tr+s,tc+s)
我们L骨牌覆盖的中心区域坐标为：(tr+s-1,tc+s-1),(tr+s-1,tc+s),(tr+s,tc+s-1),(tr+s,tc+s);

这里我们以右上子棋盘递归为例,剩下的三个子棋盘只需要找到相应的坐标替换即可。
如果特殊方格在右上子棋盘中,只需要将方格左上角坐标替换为(tr,tc+s),
否则我们用一个变量t记下此时L型骨牌序号,并将对应的中心坐标用board[][]数组记下
这里我们选的是右上,所以board[tr+s-1][tr+s]=t;
这里我们这一层递归对应的L型骨牌的t是一样的,然后我们再递归这一情况。
注意：此时不仅子方格坐标已经改变,特殊方格坐标也已经改变。此时右上的特殊方格坐标更新为：(tr+s-1,tc+s)。
递归这个过程我们就完成了一个子方格的覆盖操作,然后再去覆盖其它3个子方格进行同样的操作，只需更改一下坐标即可。
附代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int board[1005][1005];
int tile=1;
void ChessBoard(int tr,int tc,int dr,int dc,int size) {
	if(size==1)
		return ;
	int t=tile++;
	int s=size/2;
	//Upper Left Corner
	if(dr<tr+s&&dc<tc+s)//Special grid in board
		ChessBoard(tr,tc,dr,dc,s);
	else {//Special grid not in board
		board[tr+s-1][tc+s-1]=t;
		ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
	}
	//Upper Right Corner
	if(dr<tr+s&&dc>=tc+s)
		ChessBoard(tr,tc+s,dr,dc,s);
	else {
		board[tr+s-1][tc+s]=t;
		ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
	}
	//Bottom Left Corner
	if(dr>=tr+s&&dc<tc+s)
		ChessBoard(tr+s,tc,dr,dc,s);
	else {
		board[tr+s][tc+s-1]=t;
		ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
	}
	//Bottom Right Corner
	if(dr>=tr+s&&dc>=tc+s)
		ChessBoard(tr+s,tc+s,dr,dc,s);
	else {
		board[tr+s][tc+s]=t;
		ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
	}
}
int main() {
	int k,x,y;
	while(~scanf("%d",&k)) {
		memset(board,0,sizeof(board));
		int n=1<<k;
		scanf("%d%d",&x,&y);
		board[x][y]=-1;
		ChessBoard(1,1,x,y,n);
		for(int i=1; i<=n; i++) {
			for(int j=1; j<=n; j++) {
				printf("%d ",board[i][j]);
			}
			printf("\n");
		}
	}
	return 0;
}

Input:
2
2 2
Output:
2 2 3 3
2 -1 1 3
4 1 1 5
4 4 5 5