树状数组

树状数组

对于一个数组，我们如果要求区间[l,r]之间求和，我们可以采用前缀和相减的方式，也就是a[r]-a[l-1];
这里数组中的元素都是静态的，但如果我们对数组中的元素进行修改，那么我们该怎么进行求解呢？我们暴力求解的时间复杂度为O(n),如果我们有n次查询，时间复杂度是O(n^2)，这是很高的，所以我们为了降低时间复杂度，我们引入树状数组。

我们看下面这张图：

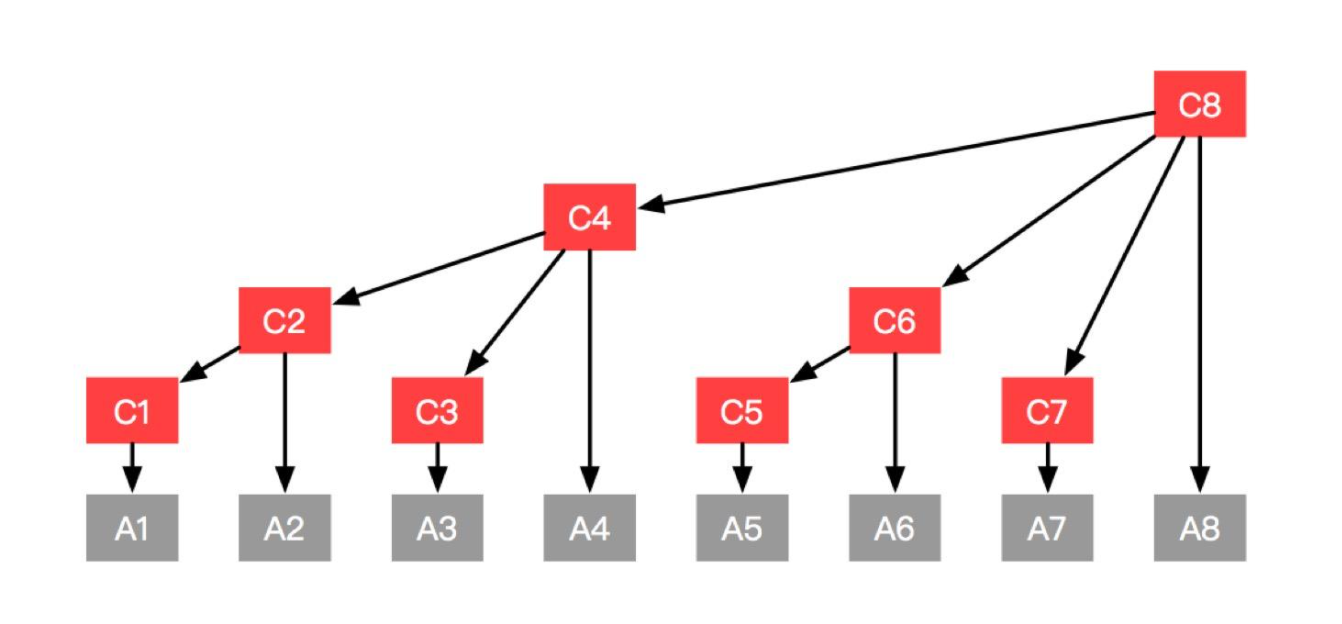
对于每一个c[x]，它的长度都是lowbit(x)，lowbit函数返回的是这个数二进制下最后一个1的位置。我们以c[6]和c[8]为例，6的二进制为110，那么他的长度为2^1=2(末位有多少个0),c[6]=a[5]+a[6];8的二进制为1000，那么他的长度为2^3=8，c[8]=a[1]+a[2]+…+a[8]。

我们再看一张图：

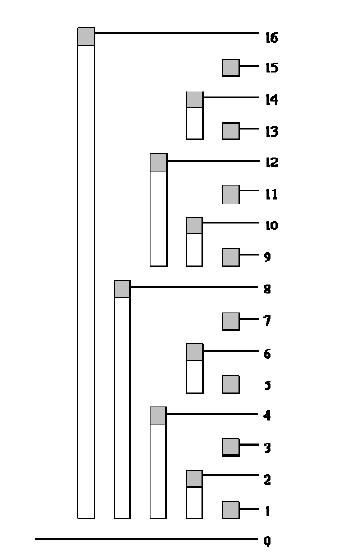
如果我们要求前14项的和我们只需要查找c[14]（2^1的区间长度）,c[12]（2^2的区间长度）,c[8]（2^3的区间长度）即可，我们对照二进制发现14为1110，每次只需要将末位的1变成0也就是x-=lowbit(x)即可得到前缀和。14对应二进制变化为1110->1100->1000->0000。

我们要对某个值进行更新，显然不能只对这一点的树状数组更新，而是要对所有包含该点的树状数组进行更新，例如我们要对a[6]进行更新，那么我们要对c[6],c[8],c[16]进行更新，我们对照二进制发现，每次查找的元素下标为x+=lowbit(x),即可进行更新。6对应的二进制变化为110->1000->10000。

单点更新区间查询

最简单的树状数组操作：

#include<stdio.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int c[N];
int a[N];
int n;
int lowbit(int x) {
	return x&(-x);
}
int sum(int x) {
	int res=0;
	while(x>0) {
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
void update(int x,int val) {
	while(x<=n) {
		c[x]+=val;
		x+=lowbit(x);
	}
}
int main() {
	int q,pos,x;
	scanf("%d",&n);
	for(int i=1; i<=n; i++) {
		scanf("%d",&a[i]);
		update(i,a[i]);
	}
	scanf("%d",&q);
	/*for(int i=1; i<=n; i++)
		printf("%d ",sum[i]);
	puts("");*/
	while(q--) {
		scanf("%d%d",&pos,&x);
		update(pos,x);
		for(int i=1; i<=n; i++)
			printf("%d\n",sum(i));
	}
	return 0;
}

附一道题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1166

区间更新单点查询

首先我们来看一下差分数组，我们设定一个数组a[]={3,5,2,4,8},那么他的差分数组为b[]={3,2,-3,2,4}，易证a[i]=b[1]+b[2]+....+b[i]，即差分数组的前缀和为对应原数组的元素。如果我要对原数组中[2,4]区间中的每个元素+2，我们来看一下a[]={3,7,4,6,8},b []={3,4,-3,2,2}; 我们发现差分数组中只有b[2]和b[5]的值改变，且b[2]增加2，b[5]减少2,也就是说我们在对区间更新时，只需对差分数组b[l]+val,b[r+1]-val即可，再求区间和的时候需要跑一遍前缀和，但这是时间复杂度为O(1)的更新，O(n)的查询。所以我们需要对差分数组用树状数组维护一下，将时间复杂度降到O(logn)。

#include<stdio.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int a[N],b[N],c[N];
int n;
int lowbit(int x) {
	return x&(-x);
}
int sum(int x) {
	int res=0;
	while(x>0) {
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
void update(int x,int val) {
	while(x<=n) {
		c[x]+=val;
		x+=lowbit(x);
	}
}
int main() {
	int q,l,r,x,k,pos;
	scanf("%d",&n);
	for(int i=1; i<=n; i++) {
		scanf("%d",&a[i]);
		b[i]=a[i]-a[i-1];
		update(i,b[i]);
	}
	scanf("%d",&q);
	while(q--) {
		scanf("%d%d%d",&l,&r,&x);
		update(l,x);
		update(r+1,-x);
	}
	scanf("%d",&k);
	while(k--)
	{
		scanf("%d",&pos);
		printf("%d\n",sum(pos));
	}
	return 0;
}

这里有一些习题可供练习：
POJ 2352
CodeForces #755D
HDU 1166
HDU 1556
BZOJ 1878
BZOJ 2743
BZOJ 1452

单点更新 区间查询

区间更新 单点查询

单点更新区间查询

区间更新单点查询