HappyCpp

一个不会打代码的程序猿

0%

kmp

发表于 分类于 阅读次数： 评论数：

kmp

暴力寻找子串

对于一个源串和一个模式串，我们要查找模式串在源串中出现第一次的位置。
我们最简单的想法是进行暴力求解，即遍历源串当中的每一个字符，去进行判断从这个字符开始能否组成模式串。
我们设源串的长度为n，模式串的长度为m，这样的话我们遍历一遍的时间复杂度是O(n*m)，
当n或m较大时，此时这种方法就会很慢，所以我们要对其进行优化。
我们先给出暴力求解的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int baoli_str(char s[],char p[],int n,int m) {
	int i=0,j=0;
	int sc=0;
	while(i<n) {
		if(s[i]==p[j]) {
			i++;
			j++;
			if(j==m)
				return sc;
		} else {
			sc++;
			i=sc;
			j=0;
		}
	}
	return -1;
}

kmp

kmp是一种改进的字符串匹配算法，他的核心时求出模式串中的next数组，再让模式串去匹配源串
我们先来看next数组的求解：
next的数组表示的是从模式串的其实位置到当前位置-1的前缀和后缀相等字符的最大数量。
我们来看这么一个串abcabb,next[0]=-1;我们可以轻松的得到next数组的数值，如下图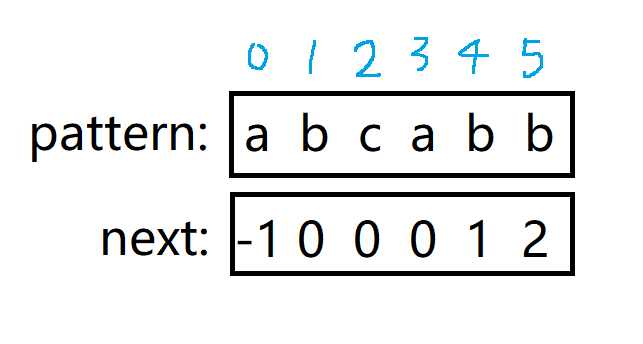

我们设定两个指针i,j,其中i表示模式串的当前位置，j表示已经匹配的前缀串的最后一个位置。
next[1]:j=-1,i=0;我们让i++,j++,此时next[1]=0;
next[2]:j=0,i=1;因为p[i]!=p[j],所以我们需要向前回溯在已经匹配好的字符串继续寻找，也就是让j=next[2]，看能否满足p[i]==p[j]，直到找到或j为-1为止。
next[3]:j=0,i=2;p[i]!=p[j],回溯,next[3]=0。
next[4]:j=0,i=3;p[i]=p[j],next[4]=1。
next[5]:j=1,i=4;p[i]=p[j],next[5]=2。
下面这张图详细讲解了回溯的过程(非上面的例子):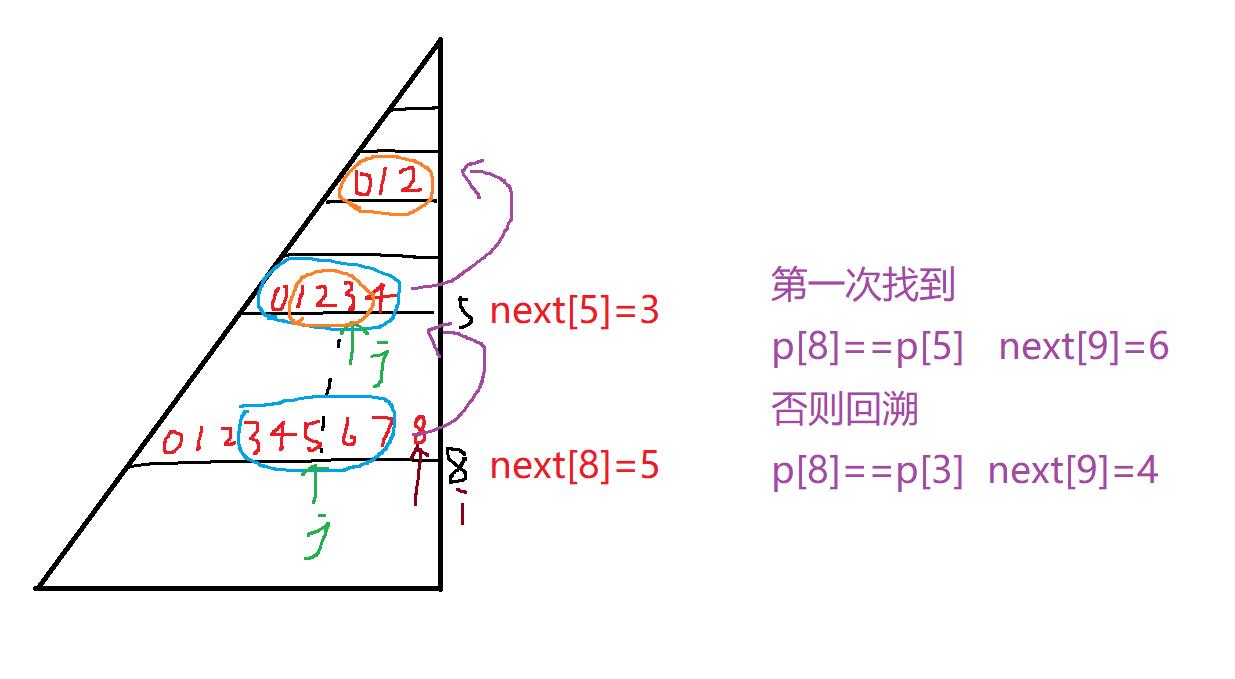

j指针不断回溯到当前串中匹配的好的串中去寻找能否有让p[i]==p[j]，因为在回溯过程中前缀串的长度不断减少，且这些回溯的前缀串一定和现在的后缀串相等，我们只需要找到一一个满足条件的，就可以去更新next数组的值。

下面我们看一下模式串是如何匹配源串的。
我们设源串s=”abcabcabbab”,模式串p=”abcabb”。我们可以发现当匹配到第6位也就是i=5时，没有匹配上，所以我们让j回溯，因为前面的ab(后缀ab)已经匹配上了(此时next[j]!=0)，所以我需要找这一位的next[j]去找前缀ab后面的那个位置去判断是否与当前的s[i]相等即可。当next[j]=0时,说明此点前缀和后缀无重合部分，所以我们的模式串从第1位开始也就是j=0开始。若s[i]==p[j]直接让i++,j++即可，然后我们判断一下当前j是否已经将整个模式串跑完即可。

我们来看一下时间复杂度，我们求解next数组需要O(m)的时间复杂度，匹配时我们需要O(n)的时间复杂度，虽然两个方法都有回溯过程，但都是常数级的，所以我们总的时间复杂度时O(n*m)。
附代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<stdio.h>
#include<string.h>
const int N=1e6+5;
char s[N],p[N];
int next[N];
void getNext(int m) {
	int i,j;
	j=next[0]=-1;
	i=0;
	while(i<m) {
		while(j!=-1&&p[i]!=p[j])
			j=next[j];
		next[++i]=++j;
	}
}
int kmp(int n,int m) {
	int i=0,j=0;
	while(i<n) {
		while(j!=-1&&s[i]!=p[j])j=next[j];
		i++;
		j++;
		if(j>=m) {
			return i-j;
		}
	}
	return -1;
}
int main() {
	scanf("%s",s);
	scanf("%s",p);
	int n=strlen(s),m=strlen(p);
	getNext(m);
	int pos=kmp(n,m);
	printf("%d\n",pos);
	return 0;
}

附两道模板题
poj-3461
hdu-1711